
递归为难了多少人?
我记得,大学学C语言时,在函数递归调用那一节有个作业,就是写汉诺塔。不少同学遭遇到困难。在知乎上遇见的就有: 如何理解诺塔的递归?
该知乎用户发出“悲鸣”:“……学C++递归篇 看懂了斐波那契序列的递归 但是却死也看不懂移动汉诺塔……”
还有:如果看不懂汉诺塔的递归逻辑,是不是可以放弃学习编程了?
这位朋友似乎更“惨烈”,因为他仿佛被为难到怀疑起人生:“……是不是可以放弃学习编程了…?!”。虽然他学的是Python,但语言在这里与问题无关,问题还是出在对递归的理解上,还是卡在汉诺塔这个实例上。
呀,可不要轻易说和编程无缘,有时你只时差一说得相对清楚的文章而已。
来看看知乎网友的反馈:
第一招:粗暴代入最简数据——从两层塔的找规律
类似提问还有不少,而且每个问题下都有许多回答,很多图文并茂,讲得认真仔细。不过,我会觉得,如果无法把这问题极大的“本质简单化”,怕是回答越长,读起来越是“好像懂了点……自己再要想,又糊了”。
参加过信奥之类比赛的同学,肯定都知道暂无思路时的一个"土"、或称为“粗暴”但有效方法:先用简单的数据走一遍。我们也来从两层的塔看起:
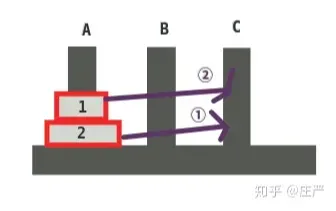
想把A柱上套着的两层“盘”按“汉诺塔”要求挪到C柱。大的思路就是:
第一步:把2号盘挪到C柱;第二步:再把1号套上去,一切OK。
可是,2号盘头上顶着1号盘,2号盘取不出来呀?那我们再增一个过渡步骤吧:把2号盘头上的1号盘取出来套到中间的B柱上,不就得了?所以,现在的思路是三步解决:
- 第一步:把 2号盘 头上的 1号盘,挪到 中间柱子 上;
- 第二步:把 2号盘 挪到 目标柱 上;
- 第三步:把(现在)位于 中间柱子 上的 1号盘,挪到 目标柱 上。
大功告成!现在,无论是理论层面,还是实践层面,我们都非常擅长玩2层的汉诺塔了。
不过,如何把这2层玩法的经验推广到更多层呢?对一个老程序员来,这太简单了;对于一个新程序员来,这也很简单,只要听老程序员一说,就一准学会:
我们要把前面(简化数据后观察到的)具体经验中的所有实际对象,抽象一下,就可以了。
第二招:基于最简单规律抽象
上面经验中,有这么些个实际对象:“2号盘”、“1号盘” 和 “中间柱子”、“目标柱” 等等。如果你没注意到,请现在抬头再往上看看。
1. 先来抽象 “2号盘”
试想,如果是套三层,它就该是3号盘了,如果是四层,它就是4号盘了,怎么办?好办呀,它其实是指“最底下的盘”呀,简称"底盘"——这就是幼儿园小朋友的抽象(这是真的,我家就读大班的小朋友,在我问他的思路时,他就是这么描述这个对象的)。
抽象到这层面已经非常够用了,唯一不足就是无法体现我们是大学生在数学知识上的优势,为此,我们可以这样抽象(并没有更好用):设有N层,则称最底下(也是最大的)那个盘,为N号盘。
2. 再来抽象 “1号盘”
有2号盘作基础,这回我们长话短说:“1号盘”可以抽象为:最底下的盘之上的所有盘。而由于这个术语有些长,所以我决定把它也称为“底盘上的那一坨”,有时也会进一步简化为:“那一坨”,特别是当底盘已经挪走后。
为什么是“所有盘”?以初始局面为例:当有三层时,那么在最大的盘(3号)的头上,难道不是2号和1号两(多)张盘吗?
这里我的五岁儿子说的“最底下盘之上的所有盘”,也可说为:N号盘上面的所有编号必然小于N的盘。同样以初始化局面为例,则为 N-1到1号盘(不一定连续)。
3. 最后抽象 “中间柱子”
这里很容易误解为:中间柱子就是A,B,C中间的 B柱。其实在后续步骤中,那可不一定。应该说,如果你在某一步骤时,想把某根柱子上“最底下的盘”挪到另一根柱子上,则称“最底下的盘”所在的柱子,为当前步骤的“源柱”,“最底下的盘”想挪至的那根柱子,称为“目标柱”,则自然有:余下的那根柱子称为“中间柱”(或者叫 过渡柱)。
第三招:把术语代入实际步骤
抽象完成,将抽象后的术语代入前面的三个步骤,得到:
- 第一步:把当前 源柱上 的 底盘上那一坨 ,挪到 中间柱子;
- 第二步:把当前 源柱上的底盘挪到目标柱;
- 第三步:把当前 中间柱子上的那一坨,挪到目标柱。
现在,我们已经掌握挪N层塔(盘)的抽象理论了,“学霸们”都知道,此时应该用这个理论,倒过来套一个具体事物,加以验证,以保正确:那我们来套一个3层的:
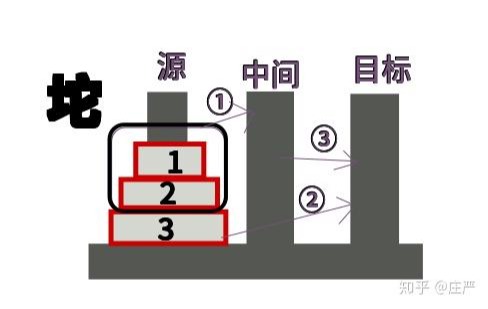
具体实践:
- 第一步:先把那一坨(1号与2号盘)挪到中间柱;
- 第二步:再把底盘(3号盘)挪到目标柱;
- 第三步:最后,把已经在中间柱上的那一坨(1号与2号盘)挪到目标柱。
非常简单!以至于我夹起人造革的包差点就想走出教室了。然后有学生叫住我,指出疑问:
第一步是违规的:不允许将多张盘(也就是老师您说的“坨”)一次性挪到另一根柱子;同理第三步也是违规的。
好,那我们就来谈谈,如何把那一坨盘(1号和2号)从源柱移到中间柱。
好,那我们就来谈谈,如何把那一坨盘(1号和2号)从源柱移到中间柱。
等等!
两张盘!从一个柱挪到另一个柱子,并且一样拥有另一根柱做中间柱子——这不就是我们一开始就搞定的事吗?
在本文开始不久,你就已经(从理论和实践上)完全掌握:
把A柱上的1号和2号盘,以B柱为中间柱,挪到C柱;
现在,你哪有可能,竟然不会下面这道题:
把A柱上的1号和2号盘,以C柱为中间柱,挪到B柱?
注意两个问题的不同,就是目标柱和中间柱做了对调而已。再看第三步。请设想1号和2盘已经叠在B柱上,所以第三步的目标就是:
把B柱上的1号盘和2号盘,以A柱为中间柱,挪到C柱。
显然,这次是 源柱和中间柱做了对调 而已。
所以,无论是第一步,还是第三步,你都可以完成的,至于第二步,它已经是最简化的一步了——别说用手,就是用嘴叼,我也能轻松将某个底盘,从一根柱子上叨出来,再套放到另一根上面去。(画面好像有些H)
第四招:归纳、拔高,找出解题本质
真正的重点,我家小朋友无法理解,只有正在学编程的你才能听懂的道理马上要来了……
让我们先理一理:
- 为了把3张盘从A挪到C……
- 我们得先将上面的2张盘从A挪到B……
- 而为了将2张盘从A挪到B……
- 我们得先将上面的1张盘,从A挪到C……
- 而为了将1张盘从A挪到C……
- 我们必须学会直立行走,从而将上肢演化发育为手;实在没手的话,嘴巴灵活一些也不是不可以……
忽略上面的第6点。看前面1到5,你发现没有:先是3张盘,发现一步解决不了,于是处理最底下的第3张盘上面的2张盘;但还是无法一步处理,于是处理2张盘上面的1张盘……于是,竟然解决了。
这就是递归——为了解决 第N个问题,需要先解决第N-1的问题,而为了解决N-1的问题,需要先解决第N-2个问题,直到解决第1个问题。而且在这其中,前面第N、第N-1、直至倒数第2个问题的解决算法,都是一致的。
什么代码都没有,你说个球?!
核心代码思路
1. 关键函数说明
1.1 top 函数
假设我有一个函数叫“top()”,当调用 top(Src) 时,它可以取到源柱(入参Src)最顶上那个盘的编号,但并不代表真的将这个盘从柱子上取出来。(原谅我中STL毒太深,显然直接取出来也能解决问题)
1.2 pop 函数
假设我有一个函数叫“pop()”,当调用 pop(Src) 时,它可以把柱子最上面的那个盘,取出来。
1.3 push 函数
假设我有一个函数叫 “push()”,当调用 push(Dst, number) 时,它可以将编号为 number 的盘子,套到目标柱上(入参Dst)。
上面以源柱和目标柱为例,实际上也有可能往中间柱上套盘子。假设以“Tmp”代表中间柱,那么当你看到 push (Tmp, 4) 时,你应该能懂,这是在把 4 号盘套到 中间柱子上。
1.4 核心操作:用 move 函数实现移动一坨
最后,假设我用 “pile” 这个单词来表达 “坨”;那么,万事具备,只欠这么一个用以表达及实现“移动”的函数了:
// 示意算法,类C的伪代码:
move (pile, Src, Tmp, Dst)
{
……在这里,把 pile 层的一坨盘子,从 Src柱,经由 Tmp柱,移到 Dst柱上……
}
这个move 怎么实现呢?当然是先实现用嘴叼都可以做的事——也就是pile为1时的情况:
// 关键的移盘函数,暂时只能挪一层的情况:
move (pile, Src, Tmp, Dst)
{
if (pile == 1) // 只有一层,用不到 Tmp
{
number = top(Src); //读到源柱上(唯一1层)盘的号码
pop(Src); //从源柱上取出
push(Dst, number); //把number号盘,套到目标柱上去。
return;
}
....
}
正如注释所说,仅有一层的情况下,直接从源柱取出来,再套进目标柱就可以了,Tmp在这种情况下没有用处。
那 pile 多于1,比如2层、3 层、4层呢?前面说了半天的结论呀,不怕麻烦,别骂我啰嗦(我的白话C++那么厚的原因,因为就是面对新人),再来看一次步骤的当下的演化:
- 第一步:先把底盘上 的 pile - 1 层那一“坨”,从当前源柱经由目标柱,移动到中间柱上
这里“经由目标柱,移到中间柱”,有些绕? 这是因为,我们此时是在 “pile”层的操作之下,要实现将其上的 pile-1 层的挪走。针对 当前的 pile时,可能C柱是目标,B柱是中间柱。但是,在移动 pile-1层,C柱成了中间柱,B柱才是目标柱。
所以,这一步,用 move 表达,就是:
/* step1: 把底盘上那一坨,挪到中间柱 */
move ( pile -1, /* 底盘上的那一坨 */,
Src, /* 源柱还是源柱 */
Dst, /* 处理pile层时的目标柱却成了处理pipe-1层的中间柱Tmp */
Tmp, /* 而处理pile层时的中间柱,成了 pipe-1 层时目标柱 */
);
- 第二步:把底盘,挪到目标柱上
因为只有一层,所以此时pile为1 进入move后,会走中间柱没有用的那个 if 分支。
/* step2: 把 底盘,挪到目标柱 */
move ( 1, // 只剩底盘,所以pile为1,进入函数会走前面已实现的那个if分支
Src,
Tmp,
Dst
);
- 第三步:把现在位于中间柱的那一坨 (pile - 1),经由源柱移动到目标柱
/* step3: 把中间柱上的 那一坨, 经由源柱,移动 目标柱上 */
move (pile - 1, // 那一坨
Tmp, // 位于中间柱上
Src, // 经由源柱...
Dst // 挪到目标柱上去
);
只要是大于一层,就走上面那三步,所以现在move的实现是:
// 关键的移盘函数,可以移任意盘数了:
move (pile, Src, Tmp, Dst)
{
if (pile == 1) // 只有一层,用不到 Tmp
{
number = top(Src); //读到源柱上(唯一1层)盘的号码
pop(Src); //从源柱上取出来
push(Dst); //套到目标柱上去。
return;
}
// 2层,或2层以上,全部是三步解决:
move(pile - 1, Src, Dst, Tmp); // 先把一坨, 经由Dst,移到 Tmp
move(1, Src, Tmp, Dst); // 再把余下的一层(底盘),经由Tmp,移到Dst
move(pile - 1, Tmp, Src, Dst); // 最后,把位于中间柱子上的一坨,经由Src,移到Dst
}
核心功能完事!
更多实现细节
这种题目,通常会给出一个最大层数限制。此处假设是10层。因为是纯C风格(通用C和C++的作业),所以给一个宏来表达这10层:
#define MAX_LEVEL 10
这种题目搞无限层是没有意义的——因为它根本无关算法的核心,要实现也不难,就是改为动态分配内存而已。
我们用:
int numbers[MAX_LEVEL];
来存储某一根柱子的可能套着的盘(存的是盘的编号:最小的盘叫1号,次小的是2号……)。不过,我们有三根柱子,所以同样以纯C代码来定义一个柱子的结构体:
typedef struct
{
int index;
int numbers[MAX_LEVEL];
int count;
} Column; /* 柱子 */
三个成员,解释如下:
- index: 前面我们称A柱、B柱、C柱……听起来像是在谈汽车,所以实际我们用的是:柱1,柱2、柱3——事实上,不需要这个号也可以解决问题,只是我们为了方便在输出信息时,带上柱子的编号。这样显然会直观很多;
- numbers[MAX_LEVEL]:核心数据,前面解释过了,请参看下一条关于 count 的解释;
- count: 表示本柱子当前实际套了几层盘子。
注意一个纯粹是实现上的细节:假设一个柱子套满10个盘,那么 numbers[0]是10,numbers[1] 是9,numbers[2] 是8 ……numbers[9] 是1。也就是说我把较大盘子的编号,存储在 numbers中索引较小的位置上。
在移动的过程,同一根柱子上套着的盘子的编号,很可能不是连续的。比如,有一根柱子上面可能在某一时刻,套着 1号、5号和7号三张盘,那么,它的numbers存储的情况是:numbers[0]为7,numbers[1]为5,numbers[2]为1,即:[7, 5, 1, 0, 0, 0, 0, 0, 0, 0]。
为了直观,我还给出一个 “draw(Column* 柱子)”的函数,它可以画出指定柱子上的所有盘。draw()会调用draw_cell(),后者用于实际画一个盘子,这里我很合情合理地偷懒了:我只输出盘子的编号(“仿真”的画法,应该是画出盘子的大小)。
但仍然是一个讲究的人,所以我给所有编号加了一对小翅膀 (大雾)。
以三层汉诺塔的前两步为例,画出来的样子如下:
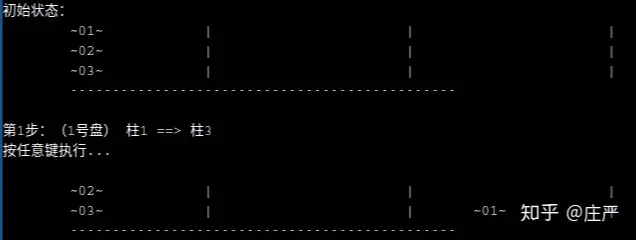
图中表达的,就是把柱1顶部的01号盘子,移动柱3。
如果,你认真研究前面的三步,你可以计算出对于 pile 层的塔,完成移动需要 2的pile次方减1步。比如,3层,就是 8-1,计7步。但这是我们人脑计算的,程序里我们让它每当走一步前面提到的“pile == 1”的分支时,就增加一次步骤。我用一个全局变量 steps 来计数。
程序有两种编译结果,代表两种运行方法,一种是全速运行,迅速给出答案;另一种是一步步演示,当你看明白某一步后,按下回车键后,(代码里不小心写成 “任意键”……)再继续下一步。代码用一个宏来区分编译:
#define STEPPING 1 // 非0编译为单步演示,为0表示全速演示
可以了吧,这样一个带有步骤输出、单步、全速双模式演示功能,兼容C/C++作业要求的汉诺塔,不用1000行,不用500行,甚至不用200行,给出来在下面了。文末还有可以在线运行演示的链接。
完整代码及在线运行
#include <stdio.h>
#define STEPPING 1 // 非0编译为单步演示,为0表示全速演示
#define MAX_LEVEL 10 // 最大层数
typedef struct
{
int index;
int numbers[MAX_LEVEL];
int count;
} Column;
Column A, B, C; // 三个柱子
int steps; // 用来累计步骤
// 初始化三根柱子,A柱将作为起始的源柱,
// 其上套好了由入参 levels_count 指定层数的盘子
void init(int levels_count)
{
steps = 0;
A.count = B.count = C.count = 0;
A.index = 1;
B.index = 2;
C.index = 3;
for (int number = levels_count; number > 0; --number)
{
A.numbers[A.count] = number;
A.count++;
B.numbers[number] = C.numbers[number] = 0; //B,C柱填0(本行删除估计也没影响)
}
}
int top(Column* src)
{
return src->numbers[src->count - 1];
}
void push(Column *dst, int number)
{
dst->numbers[dst->count] = number;
++dst->count;
}
void pop(Column *src)
{
src->numbers[src->count - 1] = 0;
--src->count;
}
void draw_cell(int number)
{
if (number > 0)
{
printf("\t~%02d~\t\t|", number);
}
else
{
printf("\t \t\t|");
}
}
void draw()
{
int row_count = A.count;
if (row_count < B.count)
{
row_count = B.count;
}
if (row_count < C.count)
{
row_count = C.count;
}
for (int i=row_count-1; i >= 0; --i)
{
draw_cell(A.numbers[i]);
draw_cell(B.numbers[i]);
draw_cell(C.numbers[i]);
printf("\n");
}
printf("\t----------------------------------------------\n");
}
void move(int pile, Column *src, Column *tmp, Column *dst)
{
if (pile == 1)
{
int number = top(src);
printf("\n第%d步:(%d号盘) 柱%d ==> 柱%d\n"
, ++steps, number, src->index, dst->index);
#if STEPPING
printf("按任意键执行...\n");
getchar();
#endif
pop(src);
push(dst, number);
draw();
return;
}
move(pile - 1, src, dst, tmp);
move(1, src, tmp, dst);
move(pile - 1, tmp, src, dst);
}
int main()
{
int levels = 0;
printf("请输入汉诺塔共几层(1~10):");
scanf("%d", &levels);
if (levels <= 0 || levels > 10)
{
printf("非法的层数:%d。", levels);
return -1;
}
getchar();
init(levels);
printf("初始状态:\n");
draw();
move(levels, &A, &B, &C);
printf("\n======[大功告成]=======\n");
printf("[%d层]汉诺塔移动完成,共%d步。\n", levels, steps);
return 0;
}
在线运行(时间长了后,链接可能会失效):